在不确定图(uncertain graph)中结合Bron-Kerbosch算法和MULE算法寻找极大团(maximal clique)

参考资料：
MULE算法
不确定图上的枚举算法研究
Bron-Kerbosch算法视频介绍
Bron-Kerbosch算法
MULE（Maximal Uncertain CLique Enumeration ）算法的论文原文是 Mining Maximal Cliques from an Uncertain Graph

论文作者：Arko Provo Mukherjee  ，Pan Xu，Srikanta Tirthapura
发表时间：2015 IEEE 31st International Conference on Data Engineering

Bron-Kerbosch算法是在确定图上找出极大团，MULE算法是在不确定图上找出极大团。
  我们现在的目的，是要在不确定图上找出极大团，现有的不确定图上极大团枚举算法中，基于顶点编号升序的典型算法—MULE 算法性能较好，其时间复杂度为 O(n·2ⁿ)。但是MULE 算法的时间代价会随着不确定图顶点规模的增大而急剧上升，而随着大数据和互联网技术的发展，不确定图的顶点规模越来越大，那么 MULE 算法也将难以满足实际应用的需求。
因此，通过将原图划分为子图，过滤掉其中绝对不可能成为 α-极大团的顶点集合，提高算法的计算效率，从而达到优化时间性能的目的。
算法的主要思想：
先不考虑原图中边上的概率，通过Bron-Kerbosch算法在原图中，找到一个个极大团子图。再对这每一个极大团子图，使用MULE算法，找出我们所需要的不确定图中的极大团。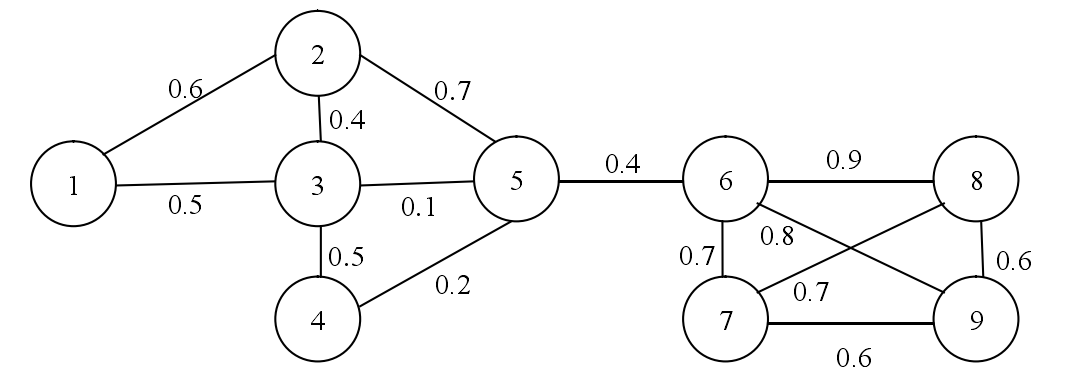

  例如这是原不确定图，在不考虑概率的情况下，我们利用Bron-Kerbosch算法可以得到5个极大团子图，分别是{1，2，3}、{2，3，5}、{3，4，5}、{5，6}、{6，7，8，9}。
  接下来对每一个极大团子图调用 MULE 算法，枚举其中的 α-极大团（这里给定α=0.1，团概率大于等于0.1的就是α-极大团，团概率就是团中每条边上权值的乘积）对于顶点集合{1，2，3}所代表的极大团子图，调用 MULE 算法，可得顶点集合{1，2，3}本身就是一个 α-极大团；对于顶点集合{2，3，5}所代表的极大团子图，调用 MULE 算法，可得顶点集合{2，3}、{2，5}以及{3，5}是 α-极大团；对于顶点集合{3，4，5}所代表的极大团子图，调用 MULE 算法，可得顶点集合{3，4}、{3，5}以及{4，5}是 α-极大团；对于顶点集合{5，6}所代表的极大团子图，调用 MULE 算法，可得顶点集合{5，6}本身就是一个 α-极大团；对于顶点集合{6，7，8，9}所代表的极大团子图，调用 MULE 算法，可得顶点集合{6，7，8，9}本身就是一个 α-极大团。因此，在对每一个极大团子图调用 MULE 算法后，得到的所有 α-极大团为{1，2，3}、{2，3}、{2，5}、{3，5}、{3，4}、{3，5}、{4，5}、{5，6}以及{6，7，8，9}共计 9 个 α-极大团。
  在原图中，给定 α = 0.1，那么不确定图 G 中的 α-极大团分别为顶点集合{1，2，3}、{2，5}、{3，4}、{3，5}、{4，5}、{5，6}以及{6，7，8，9}，共 7 个 α-极大团。可是现在有了9个，多出了两个，这多出的两个，可以通过验证算法去掉，以后再详细介绍，这里不考虑，我只需要求出最后的9个极大团，就算完成任务。
下面是代码：
头文件：

Vertex_Value.h
#pragma once
#include <iostream>
using namespace std;
//这个相当于临接表中的边界点
class Vertex_Value
{
public:
	Vertex_Value(void);
	~Vertex_Value(void);
	Vertex_Value(int x, float y);

public:
	int vertex;  //邻接表中边结点的编号
	float val;    //结点之间的概率
};

node.h
#pragma once
#include "Vertex_Value.h"
#include <vector>
using namespace std;
//相当于头结点
class node
{
public:
	int vertex;    //头节点的结点编号
	vector<Vertex_Value> vec;  //这里用vector动态数组来放边结点，Vertex_Value表示边结点，其中有结点编号，以及边上的概率
};

UDG.h
#pragma once
#include "Vertex_Value.h"
#include <vector>
using namespace std;
//相当于头结点
class node
{
#pragma once
#include "node.h"

class UDG
{
public:
	int vernum, arcnum;
	node *AdjVector;//是邻接vector的形式 一个数组名字叫AdjVector,数组里面存放的是node形式的的数据
};

ReadFile.h
#pragma once
#include "UDG.h"

#define path "F:\\c++_code\\test2.txt"
//读取文件
class ReadFile
{
public:
	ReadFile(void);
	~ReadFile(void);
	void CreateUdg(UDG &g); //读取文件后，构建出不确定图出来
};

BasicFunctions.h
#pragma once
#include <vector>
#include "UDG.h"
#include "Vertex_Value.h"
using namespace std;

#define $ 0.1 //概率阈值，极大团的团概率要大于这个值
class BasicFunctions
{
public:
	BasicFunctions(void);
	~BasicFunctions(void);

	vector<UDG> Bron_Kerbosch(const UDG g);//把不确定图作为确定图来看待，得到所有的极大团子图

	void MULE(const UDG g);//在不确定图g中，找到所有团概率大于阈值的极大团

	void EnumUncertainMC(vector<int> C, float q, vector<Vertex_Value> I, vector<Vertex_Value>& X, UDG g);//在MULE算法中枚举图中的极大团

	vector<Vertex_Value> GenerateI(vector<int> C, float q, vector<Vertex_Value> I, UDG g);//在MULE算法中，用来更新I集合

	vector<Vertex_Value> GenerateX(vector<int> C, float q, vector<Vertex_Value> X, UDG g);//在MULE算法中，用来更新X集合

	void fuzhufunction(vector<int> C, float q, vector<Vertex_Value> I, vector<Vertex_Value>& X, int i, UDG g);//在MULE算法中的辅助函数

	bool IfConnect(int u, int v, UDG g);  //判断在图g中，结点u和结点v是否连接

	void Enum_Deterministic(vector <int> all, vector <int> some, vector <int> none, UDG g);//用在Bron_Kerbosch算法中，枚举图中的极大团

	vector<int> GenerateSome(vector <int> all, vector <int> some, UDG g);//用在Enum_Deterministic中，更新其中的some集合

	vector<int> GenerateNone(vector <int> all, vector <int> none, UDG g);//用在Enum_Deterministic中，更新其中的none集合

	int MaxC(vector<int> C);//找当前团C中的最大顶点编号

	vector<int> AdjVertex(int m, UDG g);//找到图g中，m结点的所有邻接点

	vector<int> mixede(vector<int> A, vector<int> B);//求两个vector的交集

	bool isbelongto(int m, vector<int> S1);//检测m顶点是否属于S1；

	float FindValue(int u, int v, UDG g);//给定顶点对，找权值

	float clq(vector<int> C, float q, Vertex_Value D, int m, UDG g);//求当前团加入一个顶点后的团概率

	vector<int> AdjVertex_MULE(int m, UDG g);//在MULE中使用，找到m的所有邻居结点

	float FindValue_MULE(int u, int v, UDG g);//在MULE中使用，找到结点u和结点v之间的权值
};

下面是cpp文件：

Vertex_Value.cpp
#include "Vertex_Value.h"

Vertex_Value::Vertex_Value(void)
{
}

Vertex_Value::~Vertex_Value(void)
{
}
Vertex_Value::Vertex_Value(int x, float y)
{
	vertex = x;
	val = y;
}

ReadFile.cpp
#include "ReadFile.h"
#include <fstream>
#include <iostream>
using namespace std;

ReadFile::ReadFile(void)
{
}

ReadFile::~ReadFile(void)
{
}
void ReadFile::CreateUdg(UDG &g)
{
	ifstream infile(path);      //读取path里面的文本
	cout << "开始读入文件！" << endl;
	infile >> g.vernum >> g.arcnum;   //infile在这里就类似cin操作，cin是读取键盘输入，而infile是读取文件输入 >> 操作返回的是左操作数，也就是给g.vernum和g.arcnum赋值了
	cout << "顶点个数和边数为：" << endl;
	cout << g.vernum << ' ' << g.arcnum << endl;
	g.AdjVector = new node[g.vernum + 1];//0号不存结点，能储存g.vernum个结点的数组AdjVector，g.AdjVector[0]中不存放数据
	cout << "开始读入边，建立邻接vector！" << endl;
	int i;
	for (i = 0; i < g.arcnum; i++)
	{
		int head, tail;
		float val;
		infile >> head >> tail >> val;  //文本里读取文件到空格结束，循环结束以后进入到下一行
		g.AdjVector[head].vertex = head;   //这样可以完成顺序存放，这样g.AdjVector[1]中，存放的是头节点为1的结点，其他结点也都是对应的
		Vertex_Value temp;
		temp.vertex = tail;
		temp.val = val;
		g.AdjVector[head].vec.push_back(temp);
	}
}

BasicFunctions.cpp

#include<algorithm>
#include <iterator> 
#include "UDG.h"
#include "BasicFunctions.h"

vector<UDG> Amc;//用来装Bron_Kerbosch算法产生的极大团子图


BasicFunctions::BasicFunctions(void)
{
}

BasicFunctions::~BasicFunctions(void)
{
}


//***********************************************************************
//判断在图g中结点u和结点v是否相连
bool BasicFunctions::IfConnect(int u, int v, UDG g)
{
	int i;
	unsigned int j;
	for (i = 1; i <= g.vernum; i++)
	{
		if (g.AdjVector[i].vertex == u)
		{
			break;
		}
	}

	for (j = 0; j < g.AdjVector[i].vec.size(); j++)
	{
		if (v == g.AdjVector[i].vec[j].vertex)
		{
			//cout << "结点" << u << "和结点" << v << "相连" << endl;
			return true;
		}
	}
	//cout << "结点" << u << "和结点" << v << "不相连" << endl;
	return false;
}


//***********************************************************************
//检测m顶点是否属于S1；
bool BasicFunctions::isbelongto(int m, vector<int> S1)
{
	for (unsigned int i = 0; i < S1.size(); i++)
	{
		if (m == S1[i])
		{
			return true;
		}
	}
	return false;
}


//***********************************************************************
//求两个vector的交集
vector<int> BasicFunctions::mixede(vector<int> A, vector<int> B)
{
	vector<int> v;
	sort(A.begin(), A.end());
	sort(B.begin(), B.end());
	set_intersection(A.begin(), A.end(), B.begin(), B.end(), back_inserter(v));//求交集 ,必须引入<algorithm>、<iterator>才能使用这些函数
	return v;

}


//***********************************************************************
//找当前团C中的最大顶点编号
int BasicFunctions::MaxC(vector<int> C)
{
	if (C.empty())
	{
		return 0;
	}
	int max = 1;
	unsigned int i;
	for (i = 0; i < C.size(); i++)
	{
		if (max < C[i])
		{
			max = C[i];
		}
	}
	return max;
}

//***********************************************************************
//找到图g中，m结点的所有邻接点
vector<int> BasicFunctions::AdjVertex(int m, UDG g)
{
	vector<int> C;
	unsigned int i;
	for (i = 0; i < g.AdjVector[m].vec.size(); i++)
	{
		C.push_back(g.AdjVector[m].vec[i].vertex);
	}
	return C;
}


//***********************************************************************
//找到图g中，m结点的所有邻接点
vector<int> BasicFunctions::AdjVertex_MULE(int m, UDG g)
{
	vector<int> C;
	int i;
	unsigned int j;
	for (i = 1; i <= g.vernum; i++)
	{
		if (g.AdjVector[i].vertex == m) break;
	}
	for (j = 0; j < g.AdjVector[i].vec.size(); j++)
	{
		C.push_back(g.AdjVector[i].vec[j].vertex);
	}
	return C;
}

//***********************************************************************

float BasicFunctions::FindValue_MULE(int u, int v, UDG g)
{
	unsigned int i;
	int j;
	for (j = 1; j <= g.vernum; j++)
	{
		if (g.AdjVector[j].vertex == u) break;
	}

	for (i = 0; i < g.AdjVector[j].vec.size(); i++)
	{
		if (g.AdjVector[j].vec[i].vertex == v)
		{
			return g.AdjVector[j].vec[i].val;
		}
	}
	return 0;
}

//***********************************************************************
//找到图g中，结点u和结点v之间的权值
float BasicFunctions::FindValue(int u, int v, UDG g)
{
	unsigned int i;

	for (i = 0; i < g.AdjVector[u].vec.size(); i++)
	{
		if (g.AdjVector[u].vec[i].vertex == v)
		{
			return g.AdjVector[u].vec[i].val;
		}
	}
	return 0;
}
//***********************************************************************
//这个是求，如果将结点D加入加入极大团C后，团概率会变成什么值
float BasicFunctions::clq(vector<int> C, float q, Vertex_Value D, int m, UDG g)
{
	float temp;
	temp = FindValue_MULE(D.vertex, m, g);
	return q * D.val * temp;
}


//***********************************************************************
//在MULE算法中，用来更新X集合
vector<Vertex_Value> BasicFunctions::GenerateX(vector<int> C, float q, vector<Vertex_Value> X, UDG g)
{
	if (X.empty())
	{
		return X;
	}
	int m = MaxC(C);
	vector<int> S2 = AdjVertex_MULE(m, g);
	vector<Vertex_Value> _X;
	vector<int> S1;
	unsigned int i;
	for (i = 0; i < X.size(); i++)
	{
		S1.push_back(X[i].vertex);
	}
	S1 = mixede(S1, S2);
	unsigned int j;
	for (i = 0, j = 0; i < X.size(); i++)
	{
		if (isbelongto(X[i].vertex, S1))
		{
			if (clq(C, q, X[i], m, g) >= $)
			{
				_X.push_back(X[i]);
				_X[j].val = _X[j].val * FindValue_MULE(_X[j].vertex, m, g);
				j++;
			}
		}
	}
	return _X;
}


//***********************************************************************
//在MULE算法中，用来更新I集合
vector<Vertex_Value> BasicFunctions::GenerateI(vector<int> C, float q, vector<Vertex_Value> I, UDG g)
{
	int m = MaxC(C);    //找到C中编号最大的点
	vector<int> S2 = AdjVertex_MULE(m, g); //在图g中找到m的邻居接点
	vector<Vertex_Value> _I;
	vector<int> S1;
	unsigned int i;
	for (i = 0; i < I.size(); i++)
	{
		S1.push_back(I[i].vertex);
	}
	S1 = mixede(S1, S2);
	unsigned int j = 0;
	for (i = 0, j; i < I.size(); i++)
	{
		if (I[i].vertex > m && isbelongto(I[i].vertex, S1))
		{
			if (clq(C, q, I[i], m, g) >= $)
			{
				_I.push_back(I[i]);
				_I[j].val = _I[j].val * FindValue_MULE(_I[j].vertex, m, g);
				j++;
			}
		}
	}
	return _I;
}


//***********************************************************************
//EnumUncertainMC中的辅助函数
void BasicFunctions::fuzhufunction(vector<int> C, float q, vector<Vertex_Value> I, vector<Vertex_Value>& X, int i, UDG g)
{
	C.push_back(I[i].vertex);
	q = q * I[i].val;
	vector<Vertex_Value> _I = GenerateI(C, q, I, g);
	vector<Vertex_Value> _X = GenerateX(C, q, X, g);
	EnumUncertainMC(C, q, _I, _X, g);
	X.push_back(I[i]);
}


//***********************************************************************
//在MULE算法中，找到满足要求的极大团
void BasicFunctions::EnumUncertainMC(vector<int> C, float q, vector<Vertex_Value> I, vector<Vertex_Value>& X, UDG g)
{
	unsigned int i;
	if (I.empty() && X.empty())
	{
		cout << "通过MULE算法产生一个极大团！" << endl;
		for (i = 0; i < C.size(); i++)
		{
			cout << C[i] << ' ';
		}
		cout << endl;
		return;
	}
	vector<int> Ctemp(C);
	for (i = 0; i < I.size(); i++)
	{
		fuzhufunction(Ctemp, q, I, X, i, g);
	}
}

//***********************************************************************
//用在Enum_Deterministic中，更新其中的none集合
vector<int> BasicFunctions::GenerateNone(vector <int> all, vector <int> none, UDG g)
{

	int m = MaxC(all);    //找到C中编号最大的点
	vector<int> S2 = AdjVertex(m, g); //在图g中找到m的邻居接点
	vector<int> _none;
	vector<int> S1;
	unsigned int i;
	for (i = 0; i < none.size(); i++)
	{
		S1.push_back(none[i]);
	}
	S1 = mixede(S1, S2);   //保证some中放的结点，都是和all中所有结点连接的


	for (i = 0; i < none.size(); i++)
	{
		if (isbelongto(none[i], S1))
		{
			_none.push_back(none[i]);
		}
	}
	return _none;


}

//***********************************************************************
//用在Enum_Deterministic中，更新其中的some集合
vector<int> BasicFunctions::GenerateSome(vector <int> all, vector <int> some, UDG g)
{


	int m = MaxC(all);    //找到all中编号最大的点
	vector<int> S2 = AdjVertex(m, g); //在图g中找到m的邻居接点
	vector<int> _some;
	vector<int> S1;
	unsigned int i;
	for (i = 0; i < some.size(); i++)
	{
		S1.push_back(some[i]);
	}
	S1 = mixede(S1, S2);   //保证some中放的结点，都是和all中所有结点连接的


	for (i = 0; i < some.size(); i++)
	{
		if (some[i] > m && isbelongto(some[i], S1))
		{
			_some.push_back(some[i]);
		}
	}
	return _some;

}


//***********************************************************************
//用在Bron_Kerbosch算法中，枚举图中的极大团
void BasicFunctions::Enum_Deterministic(vector <int> all, vector <int> some, vector <int> none, UDG g)
{
	unsigned int i;
	if (some.empty() && none.empty())    //两者都为空，则找到极大团
	{
		UDG g_t;
		g_t.vernum = all.size();
		g_t.arcnum = (all.size()*(all.size()-1));
		g_t.AdjVector = new node[all.size() + 1];
		cout << "通过Bron_Kerbosch算法产生一个极大团子图！" << endl;
		for (i = 0; i < all.size(); i++)
		{
			cout << all[i] << ' ';
			g_t.AdjVector[i + 1] = g.AdjVector[all[i]];
		}
		cout << endl;
		Amc.push_back(g_t);
		return;
	}

	vector<int> allTemp(all);   //将all中的所有值，都赋给allTemp，allTemp用来递归到下一层（去放置极大团）
	for (i = 0; i < some.size(); i++)
	{


		allTemp.push_back(some[i]);//更新下一层中的allTemp
		vector<int> _some = GenerateSome(allTemp, some, g);//产生新的some集合。要保证新的some集合，要和allTemp集合中的所有结点都连接
		vector<int> _none = GenerateNone(allTemp, none, g);//产生新的none集合。要保证新的none集合，要和allTemp集合中的所有结点都连接
		Enum_Deterministic(allTemp, _some, _none, g);   //带着新的all,some,none集合进入到下一层中

		none.push_back(some[i]);//将some[i]放入none中，表示在这一层里面，由some[i]开始的极大团，已经探索过了

		allTemp.pop_back(); //将some[i]从allTemp中拿出，开始下一轮的for循环，在下一轮的for循环中，放入新的some[i]

	}

}



//***********************************************************************
//总算法的第一步，从原图中得到所有的极大团子图
vector<UDG> BasicFunctions::Bron_Kerbosch(const UDG g)
{


	vector <int> some(g.vernum);//声明一个初始大小为g.vernum的Vertex_Value类型的向量_I，_I中存放的结点，就是预备要放入C中的
	vector<int> all;       //声明一个int型向量all，就是极大团
	vector<int> none;   //声明一个Vertex_Value型向量X ，X存放已经探索过的某结点。
	int i = 1;
	for (i; i <= g.vernum; i++)
	{
		some[i - 1] = i;   //将所有的结点编号存放在some中
	}
	Enum_Deterministic(all, some, none, g);

	return Amc;
}


//***********************************************************************
//总算法的第二步，从每个极大团子图中，找到满足概率阈值的极大团
void BasicFunctions::MULE(const UDG g)
{
	vector <Vertex_Value> _I(g.vernum);//声明一个初始大小为g.vernum的Vertex_Value类型的向量_I，_I中存放的结点，就是预备要放入C中的
	vector<int> C;       //声明一个int型向量C
	vector<Vertex_Value> X;   //声明一个Vertex_Value型向量X ，X存放已经探索过的某结点。
	int i = 1;
	for (i; i <= g.vernum; i++)   //先初始化_I，其中存放（u,r），其中u就是Vertex_Value中的vertex（表示结点的编号），r就是Vertex_Value中的val（表示将该节点加入到极大团C后，所要乘上的概率）
	{
		_I[i - 1].vertex = g.AdjVector[i].vertex;
		_I[i - 1].val = 1;   //最开始都赋值为1
	}
	float j = 1;
	EnumUncertainMC(C, j, _I, X, g);
}

下面是主函数：

#include <tchar.h>
#include "ReadFile.h"
#include "BasicFunctions.h"
#include <iostream>
using namespace std;

int _tmain(int argc, _TCHAR* argv[])
{
	UDG g;  
	ReadFile A;
	vector<UDG> Amc;
	A.CreateUdg(g);
	BasicFunctions BF;
	Amc = BF.Bron_Kerbosch(g);
	unsigned int i;

	for (i = 0; i < Amc.size(); i++)
	{
		BF.MULE(Amc[i]);
	}
	
	system("pause"); //暂停黑窗口
	return 0;

}

test2.txt如下:
9表示结点数，28表示边数（这里的1 2和2 1算不同的边）
第一位数字是头结点，第二位数字是边结点，第三个数字是边上的概率

9 28
1 2 0.6
1 3 0.5
2 1 0.6
2 3 0.4
2 5 0.7
3 1 0.5
3 2 0.4
3 4 0.5
3 5 0.1
4 3 0.5
4 5 0.2
5 2 0.7
5 3 0.1
5 4 0.2
5 6 0.4
6 5 0.4
6 7 0.7
6 8 0.9
6 9 0.8
7 6 0.7
7 8 0.7
7 9 0.6
8 6 0.9
8 7 0.7
8 9 0.6
9 6 0.8
9 7 0.6
9 8 0.6

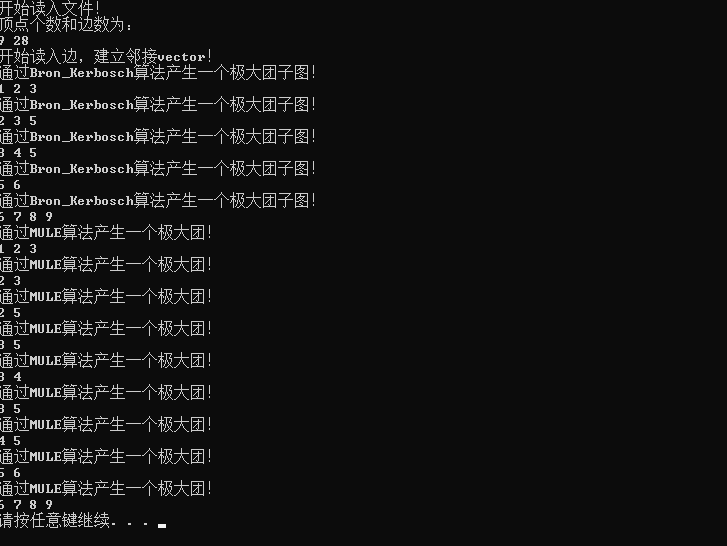
实验结果：