在不确定图(uncertain graph)中利用Bron-Kerbosch算法发现极大团(maximal clique)（另一种方法）

参考资料：
Bron-Kerbosch算法视频介绍
极大团算法
不确定图上求极大团算法
不确定图上的枚举算法研究

我们这里是把不确定图当确定图（也就是普通的图），来处理的，并没由考虑边上的概率。之所以是用的不确定图，主要是因为我最近研究的是不确定图，把不确定图的数据结构换成确定图的，也是一样的。

不确定图：
不确定图就是指边或者顶点信息中带有不确定性的图，这种不确定性通常是通过给边赋予权值来量化。用一个三元组 G=(V, E, β)表示一个不确定图，其中 β 表示边的权值，0< β <1，代表边存在的概率。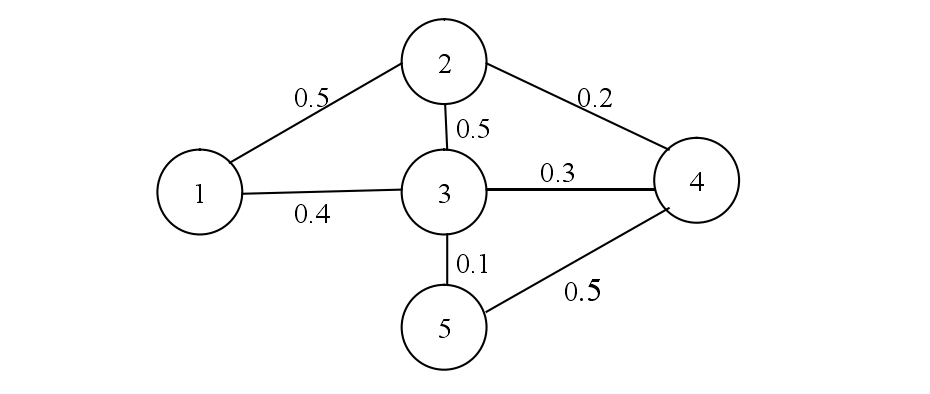

如图所示不确定图中，每一条边都拥有权值，用来表示该边在实际应用中存在的概率，所以它是一个不确定图。
1，图的存储结构用什么好？
确定为邻接vector存储结构，因为vector作为STL中的类，封装了很多函数，用起来很方便。
2，运行时遇到错误：vector subscript out of range？
应该是有vector没有分配足够的空间，但是却用了它的下标。

在我的上一篇文章里面用的思想主要是：设定关键点 pivot vertex u，只对关键点u自身和u的非邻居结点进行查找。伪代码如下：

Bron-Kerbosch Algorithm
R={}   //已确定的极大团顶点的集合
P={v}  //未处理顶点集，初始状态是所有结点
X={}   //已搜过的并且属于某个极大团的顶点集合

BronKerbosch(R, P, X):
   if P and X are both empty:
       report R as a maximal clique
   choose a pivot vertex u in P ⋃ X   //选取pivot结点u
   for each vertex v in P \ N(u):   
       BronKerbosch1(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
       P := P \ {v}
       X := X ⋃ {v}

在这个方法里的思想是：按照图顶点编号升序地往顶点集合 C 中添加顶点。例如，如果当前的顶点集合 C={1，3，4}，则当前顶点集合 C 中的最大顶点编号为 4，那么在扩展当前顶点集合 C 的过程中不需要考虑加入顶点 2，因为顶点集合{1，2，3，4}会在处理顶点 1 时按照顶点编号顺序 2，3，4 依次添加而得到。当然添加进入的顶点，必须是在C中所有顶点的公共邻居结点集合中，也就是集合P（some集合）中。

下边是头文件，大部分和上次一样，只有BasicFunctions.h会有所不同：

Vertex_Value.h
#pragma once
#include <iostream>
using namespace std;
//这个相当于临接表中的边界点
class Vertex_Value
{
public:
	Vertex_Value(void);
	~Vertex_Value(void);
	Vertex_Value(int x, float y);

public:
	int vertex;  //邻接表中边结点的编号
	float val;    //结点之间的概率
};

node.h
#pragma once
#include "Vertex_Value.h"
#include <vector>
using namespace std;
//相当于头结点
class node
{
	//public:
	//	node(void);空参的构造方法，以及析构函数可以不用写，系统会自动实现
	//	~node(void);
public:
	int vertex;    //头节点的结点编号
	vector<Vertex_Value> vec;  //这里用vector动态数组来放边结点，Vertex_Value表示边结点，其中有结点编号，以及边上的概率
};

UDG.h
#pragma once
#include "node.h"

class UDG
{
	//public:
	//	UDG(void);
	//	~UDG(void);
public:
	int vernum, arcnum;//结点数目和边的数目
	node *AdjVector;//是邻接vector的形式 一个数组名字叫AdjVector,数组里面存放的是node形式的的数据
};

ReadFile.h
#pragma once
#include "UDG.h"

#define path "F:\\c++_code\\test1.txt"//文件路径
//读取文件
class ReadFile
{
public:
	ReadFile(void);
	~ReadFile(void);
	void CreateUdg(UDG &g); //读取文件后，构建出不确定图出来
};

BasicFunctions.h里面的函数会和以前有所不同：

BasicFunctions.h
#pragma once
#include <vector>
#include "UDG.h"
#include "Vertex_Value.h"
using namespace std;

#define $ 0.1 //概率阈值，这里我把图当作是确定的，所以不考虑概率。
class BasicFunctions
{
public:
	BasicFunctions(void);
	~BasicFunctions(void);

	void Bron_Kerbosch(const UDG g);//把不确定图作为确定图来看待，得到所有的极大团子图

	bool IfConnect(int u, int v, UDG g);  //判断在图g中，结点u和结点v是否连接

	void Enum_Deterministic(vector <int> all, vector <int> some, vector <int> none, UDG g);//用在Bron_Kerbosch算法中，枚举图中的极大团

	vector<int> GenerateSome(vector <int> all, vector <int> some, UDG g);//用在Enum_Deterministic中，更新其中的some集合
	
	vector<int> GenerateNone(vector <int> all, vector <int> none, UDG g);//用在Enum_Deterministic中，更新其中的none集合

	int MaxC(vector<int> C);//找当前团C中的最大顶点编号
	
	vector<int> AdjVertex(int m, UDG g);//找到图g中，m结点的所有邻接点

	vector<int> mixede(vector<int> A, vector<int> B);//求两个vector的交集

	bool isbelongto(int m, vector<int> S1);//检测m顶点是否属于S1；

};

下面是cpp文件

Vertex_Value.cpp
#include "Vertex_Value.h"
Vertex_Value::Vertex_Value(void)
{
}

Vertex_Value::~Vertex_Value(void)
{
}
Vertex_Value::Vertex_Value(int x, float y)
{
	vertex = x;
	val = y;
}

ReadFile.cpp
#include "ReadFile.h"
#include <fstream>
#include <iostream>
using namespace std;

ReadFile::ReadFile(void)
{
}

ReadFile::~ReadFile(void)
{
}
void ReadFile::CreateUdg(UDG &g)
{
	ifstream infile(path);      //读取path里面的文本
	cout << "开始读入文件！" << endl;
	infile >> g.vernum >> g.arcnum;   //infile在这里就类似cin操作，cin是读取键盘输入，而infile是读取文件输入 >> 操作返回的是左操作数，也就是给g.vernum和g.arcnum赋值了
	cout << "顶点个数和边数为：" << endl;
	cout << g.vernum << ' ' << g.arcnum << endl;
	g.AdjVector = new node[g.vernum + 1];//0号不存结点，能储存g.vernum个结点的数组AdjVector，g.AdjVector[0]中不存放数据
	cout << "开始读入边，建立邻接vector！" << endl;
	int i;
	for (i = 0; i < g.arcnum; i++)
	{
		int head, tail;
		float val;
		infile >> head >> tail >> val;  //文本里读取文件到空格结束，循环结束以后进入到下一行
		g.AdjVector[head].vertex = head;   //这样可以完成顺序存放，这样g.AdjVector[1]中，存放的是头节点为1的结点，其他结点也都是对应的
		Vertex_Value temp;
		temp.vertex = tail;
		temp.val = val;
		g.AdjVector[head].vec.push_back(temp);
	}
}

#include<algorithm>
#include <iterator> 
#include "UDG.h"
#include "BasicFunctions.h"



BasicFunctions::BasicFunctions(void)
{
}

BasicFunctions::~BasicFunctions(void)
{
}



//***********************************************************************
//判断在图g中结点u和结点v是否相连
bool BasicFunctions::IfConnect(int u, int v, UDG g)
{
	int i;
	unsigned int j;
	for (i = 1; i <= g.vernum; i++)
	{
		if (g.AdjVector[i].vertex == u)
		{
			break;
		}
	}

	for (j = 0; j < g.AdjVector[i].vec.size(); j++)
	{
		if (v == g.AdjVector[i].vec[j].vertex)
		{
			//cout << "结点" << u << "和结点" << v << "相连" << endl;
			return true;
		}
	}
	//cout << "结点" << u << "和结点" << v << "不相连" << endl;
	return false;
}


//***********************************************************************
//检测m顶点是否属于S1；
bool BasicFunctions::isbelongto(int m, vector<int> S1)
{
	for (unsigned int i = 0; i < S1.size(); i++)
	{
		if (m == S1[i])
		{
			return true;
		}
	}
	return false;
}


//***********************************************************************
//求两个vector的交集
vector<int> BasicFunctions::mixede(vector<int> A, vector<int> B)
{
	vector<int> v;
	sort(A.begin(), A.end());
	sort(B.begin(), B.end());
	set_intersection(A.begin(), A.end(), B.begin(), B.end(), back_inserter(v));//求交集 ,必须引入<algorithm>、<iterator>才能使用这些函数
	return v;

}


//***********************************************************************
//找当前团C中的最大顶点编号
int BasicFunctions::MaxC(vector<int> C)
{
	if (C.empty())
	{
		return 0;
	}
	int max = 1;
	unsigned int i;
	for (i = 0; i < C.size(); i++)
	{
		if (max < C[i])
		{
			max = C[i];
		}
	}
	return max;
}

//***********************************************************************
//找到图g中，m结点的所有邻接点
vector<int> BasicFunctions::AdjVertex(int m, UDG g)
{
	vector<int> C;
	unsigned int i;
	for (i = 0; i < g.AdjVector[m].vec.size(); i++)
	{
		C.push_back(g.AdjVector[m].vec[i].vertex);
	}
	return C;
}

//***********************************************************************
//用在Enum_Deterministic中，更新其中的none集合
vector<int> BasicFunctions::GenerateNone(vector <int> all, vector <int> none, UDG g)
{

	int m = MaxC(all);    //找到C中编号最大的点
	vector<int> S2 = AdjVertex(m, g); //在图g中找到m的邻居接点
	vector<int> _none;
	vector<int> S1;
	unsigned int i;
	for (i = 0; i < none.size(); i++)
	{
		S1.push_back(none[i]);
	}
	S1 = mixede(S1, S2);   //保证some中放的结点，都是和all中所有结点连接的


	for (i = 0; i < none.size(); i++)
	{
		if (isbelongto(none[i], S1))
		{
			_none.push_back(none[i]);
		}
	}
	return _none;


}

//***********************************************************************
//用在Enum_Deterministic中，更新其中的some集合
vector<int> BasicFunctions::GenerateSome(vector <int> all, vector <int> some, UDG g)
{


	int m = MaxC(all);    //找到all中编号最大的点
	vector<int> S2 = AdjVertex(m, g); //在图g中找到m的邻居接点
	vector<int> _some;
	vector<int> S1;
	unsigned int i;
	for (i = 0; i < some.size(); i++)
	{
		S1.push_back(some[i]);
	}
	S1 = mixede(S1, S2);   //保证some中放的结点，都是和all中所有结点连接的


	for (i = 0; i < some.size(); i++)
	{
		if (some[i] > m && isbelongto(some[i], S1))
		{
			_some.push_back(some[i]);
		}
	}
	return _some;

}




//***********************************************************************
//用在Bron_Kerbosch算法中，枚举图中的极大团
void BasicFunctions::Enum_Deterministic(vector <int> all, vector <int> some, vector <int> none, UDG g)
{
	unsigned int i;
	if (some.empty() && none.empty())    //两者都为空，则找到极大团
	{
		cout << "产生一个极大团！" << endl;
		for (i = 0; i < all.size(); i++)
		{
			cout << all[i] << ' ';
		}
		cout << endl;
		return;
	}

	//int u = some[0];
	vector<int> allTemp(all);   //将all中的所有值，都赋给allTemp，allTemp用来递归到下一层（去放置极大团）
	for (i = 0; i < some.size(); i++)
	{

		//int v = some[i];
		//if (IfConnect(u, v, g)) continue;

		allTemp.push_back(some[i]);//更新下一层中的allTemp
		vector<int> _some = GenerateSome(allTemp, some, g);//产生新的some集合。要保证新的some集合，要和allTemp集合中的所有结点都连接
		vector<int> _none = GenerateNone(allTemp, none, g);//产生新的none集合。要保证新的none集合，要和allTemp集合中的所有结点都连接
		Enum_Deterministic(allTemp, _some, _none, g);   //带着新的all,some,none集合进入到下一层中

		none.push_back(some[i]);//将some[i]放入none中，表示在这一层里面，由some[i]开始的极大团，已经探索过了

		allTemp.pop_back(); //将some[i]从allTemp中拿出，开始下一轮的for循环，在下一轮的for循环中，放入新的some[i]

	}

}



//***********************************************************************
//总算法的第一步，从原图中得到所有的极大团子图
void BasicFunctions::Bron_Kerbosch(const UDG g)
{


	vector <int> some(g.vernum);//声明一个初始大小为g.vernum的Vertex_Value类型的向量_I，_I中存放的结点，就是预备要放入C中的
	vector<int> all;       //声明一个int型向量all，就是极大团
	vector<int> none;   //声明一个Vertex_Value型向量X ，X存放已经探索过的某结点。
	int i = 1;
	for (i; i <= g.vernum; i++)
	{
		some[i - 1] = i;   //将所有的结点编号存放在some中
	}
	Enum_Deterministic(all, some, none, g);

}

下面是主函数：

#include <tchar.h>
#include "ReadFile.h"
#include "BasicFunctions.h"
#include <iostream>
using namespace std;

int _tmain(int argc, _TCHAR* argv[])
{
	UDG g;
	ReadFile A;
	A.CreateUdg(g);
	BasicFunctions BF;
	BF.Bron_Kerbosch(g);

	system("pause"); //暂停黑窗口
	return 0;
}

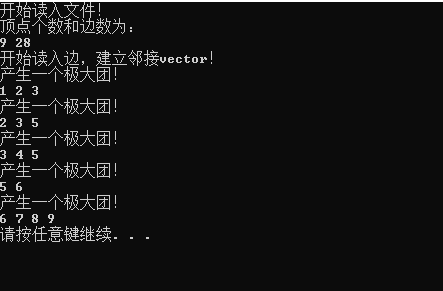
test2.txt如下:
9表示结点数，28表示边数（这里的1 2和2 1算不同的边）
第一位数字是头结点，第二位数字是边结点，第三个数字是边上的概率

9 28
1 2 0.6
1 3 0.5
2 1 0.6
2 3 0.4
2 5 0.7
3 1 0.5
3 2 0.4
3 4 0.5
3 5 0.1
4 3 0.5
4 5 0.2
5 2 0.7
5 3 0.1
5 4 0.2
5 6 0.4
6 5 0.4
6 7 0.7
6 8 0.9
6 9 0.8
7 6 0.7
7 8 0.7
7 9 0.6
8 6 0.9
8 7 0.7
8 9 0.6
9 6 0.8
9 7 0.6
9 8 0.6

实验结果：