算法导论:字典树
1 | 定义:Trie树,即字典树,又称单词查找树或键树。是一种用于快速检索的多叉树结构。 |
如果我们给定字符串集合为{b abc abd bcd abcd efg hii},那么这个字符串的字典树为: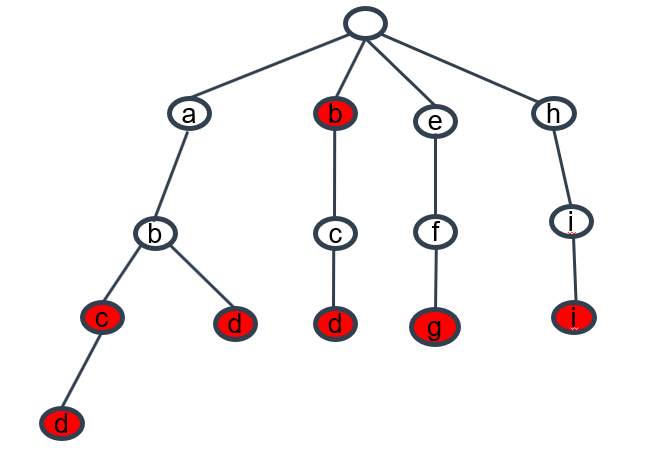
对于一颗字典树来说,应该具有以下性质:
第二条性质中的到某个结点,就是指到红色结点。
字典树的构建
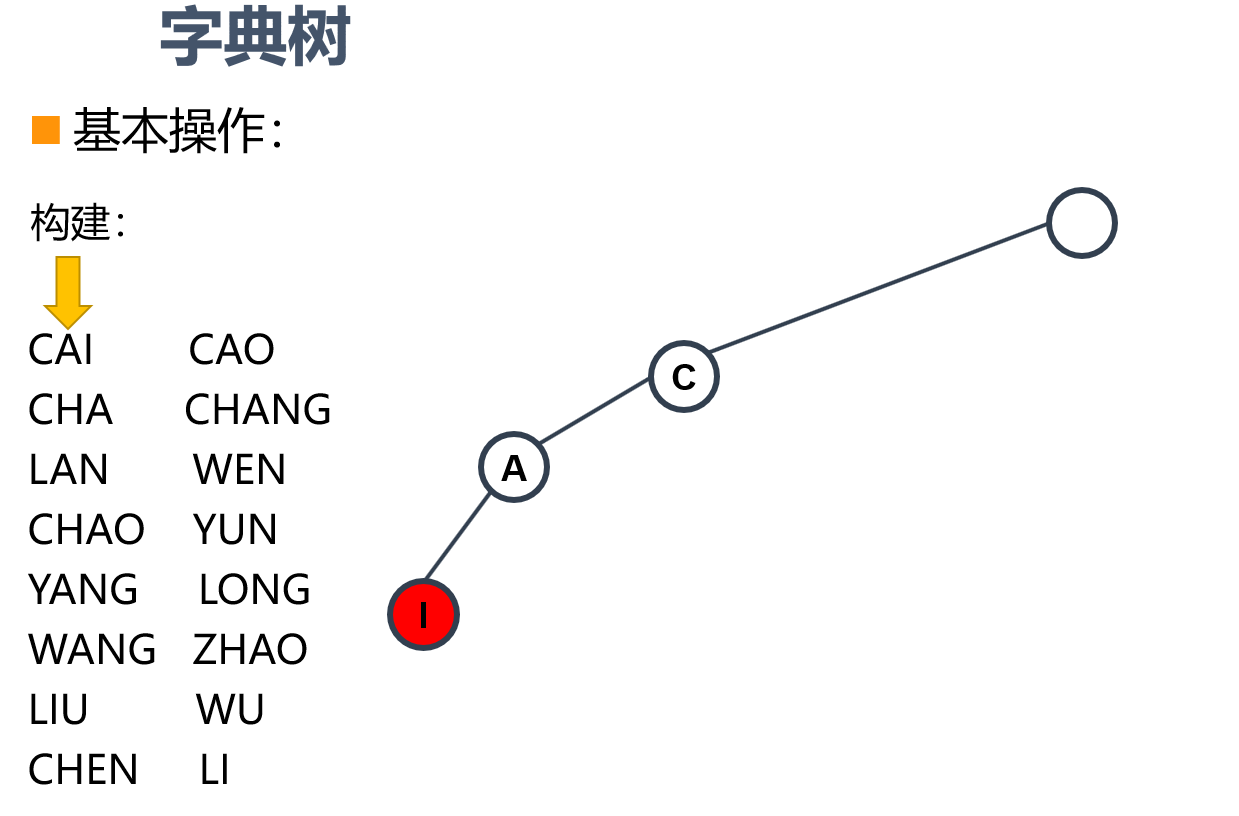
现在给出了,许多的字符串,我们从第一个字符串CAI开始构建。首先构建根节点,其次构建出CAI三个结点,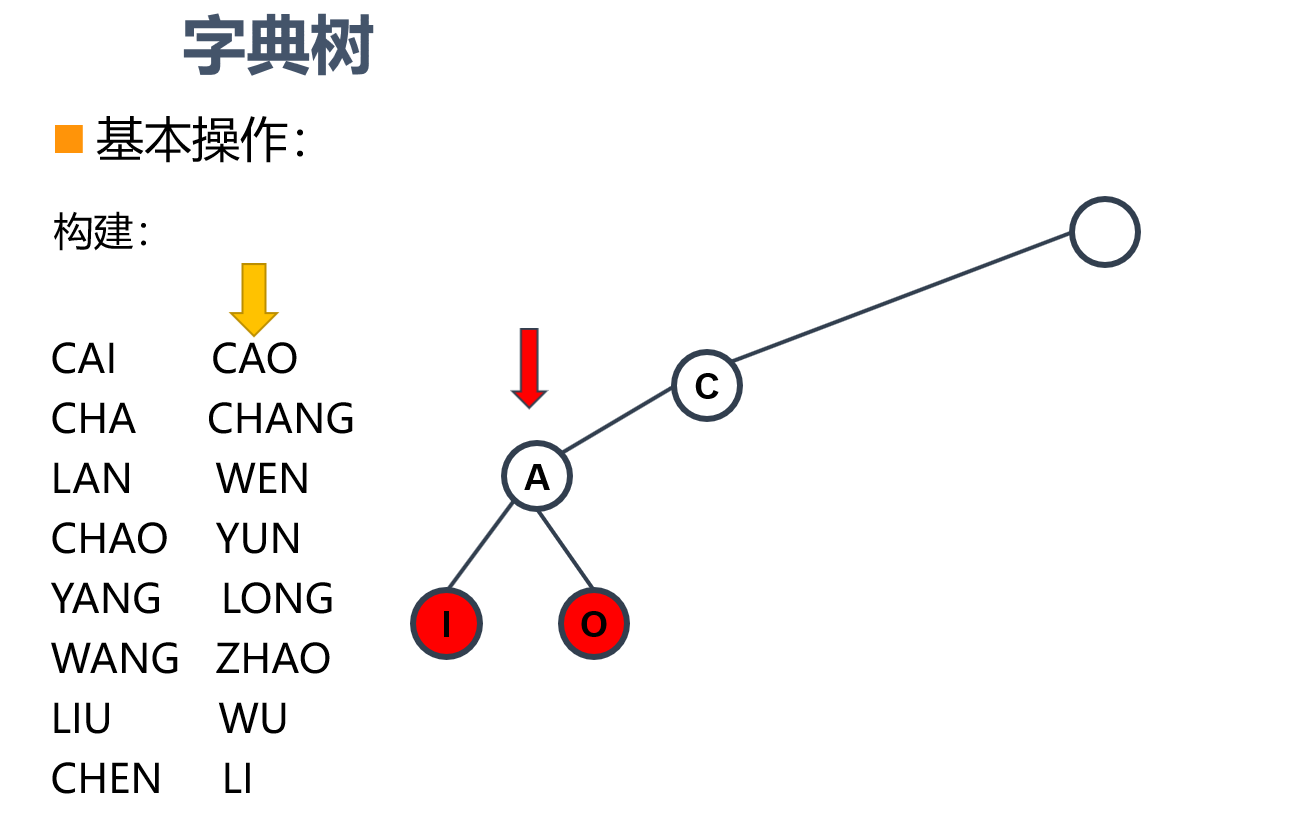
现在构建字符串CAO因为CA已经存在,所以遍历到A,发现O结点并不存在,生成O结点。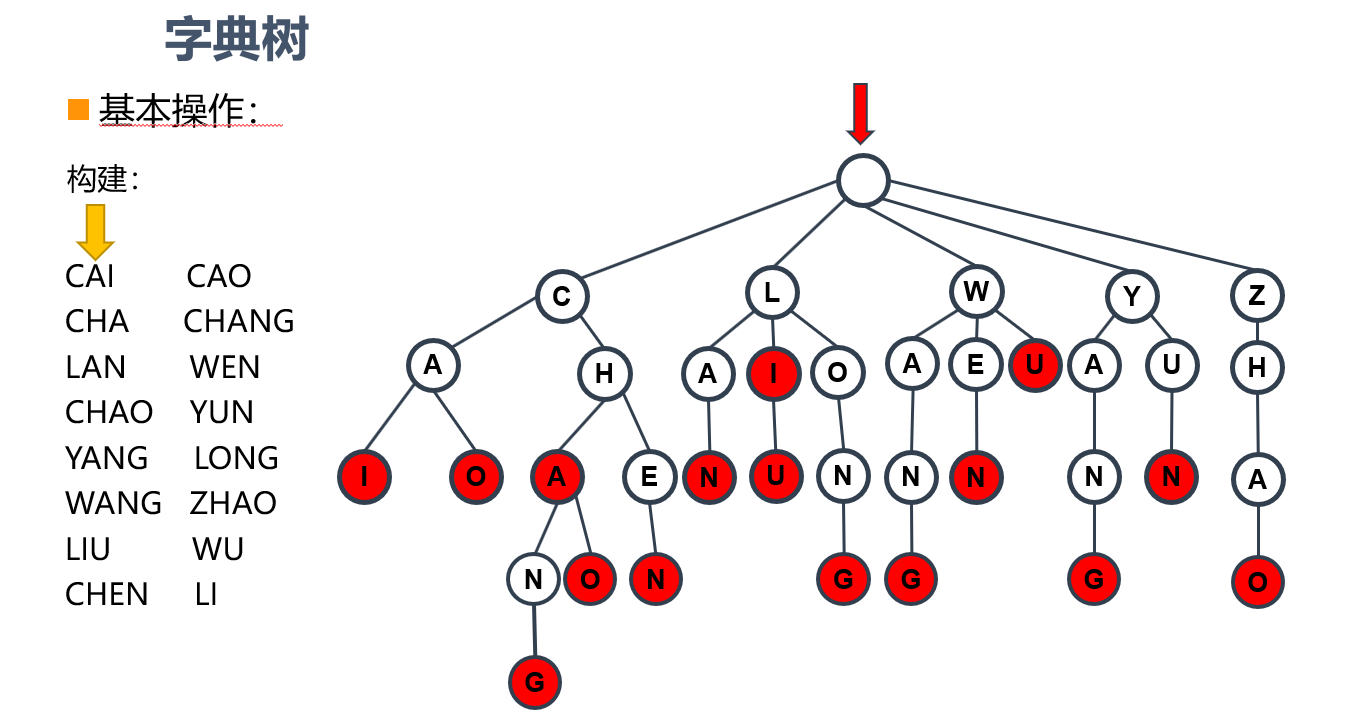
以此类推,最后生成的字典树,如上图所示。这个构建过程,每一次都相当于遍历了一个字符串的长度。
假如有n个字符串,那么它的时间复杂度就是,n乘上字符串的平均长度。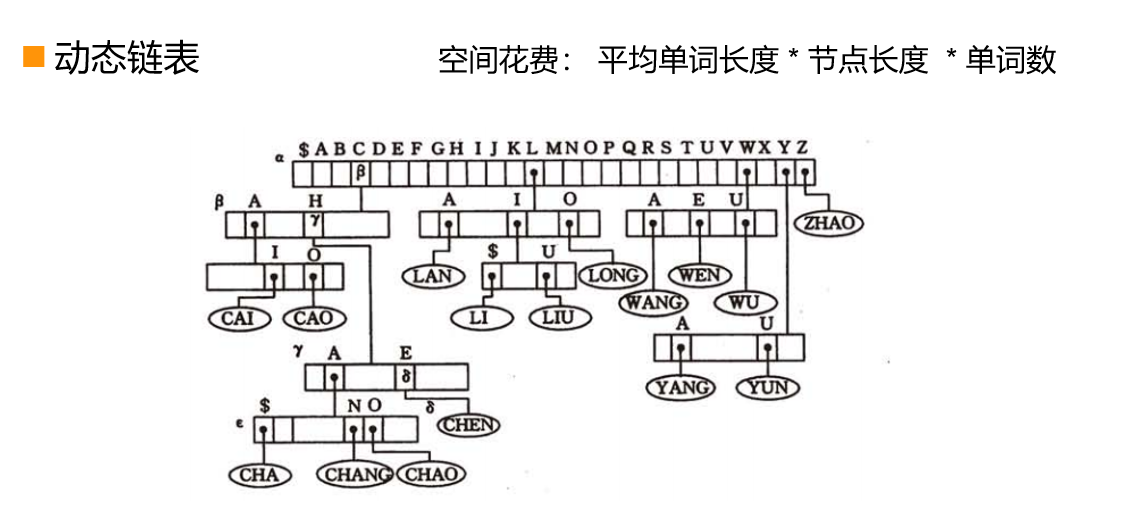
对于字典树,在空间上的花费为:
1 | 空间花费:平均单词长度*结点长度*单词数 |
字典树的查询
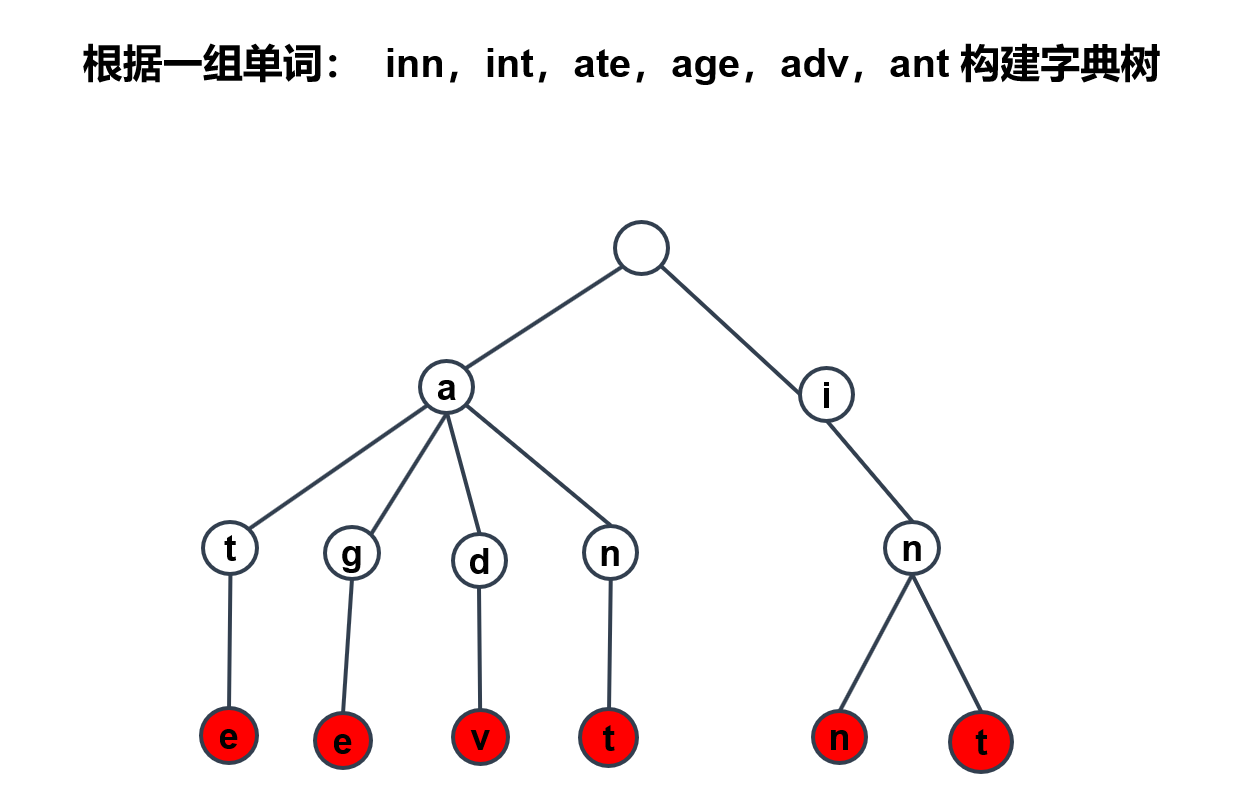
首先我们根据给出的单词,构建出了相应的字典树。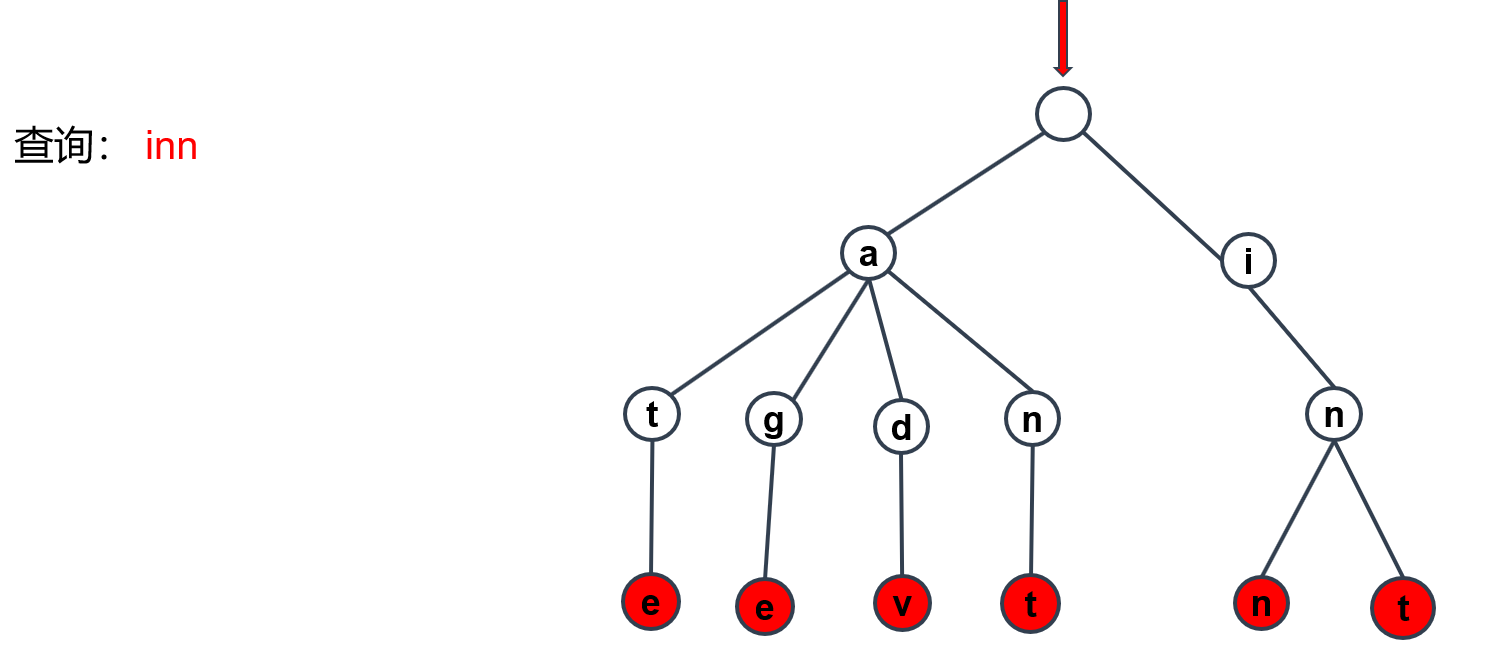
现在,我们要对inn这个单词进行查询,当然是从根节点先开始。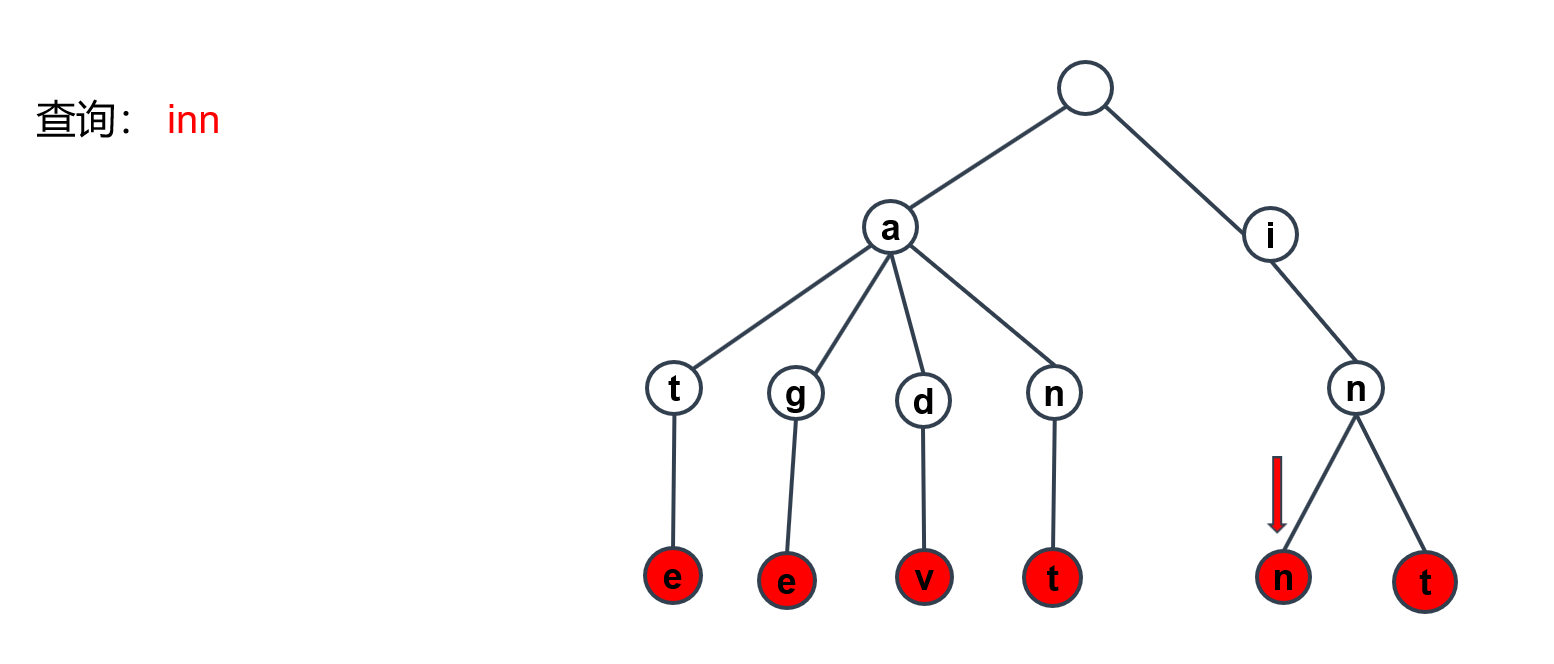
按照结点进行查询,最后可以找到inn这个字符串。那么它的时间复杂度就是这个字符串的长度O(len)。
字典树的插入
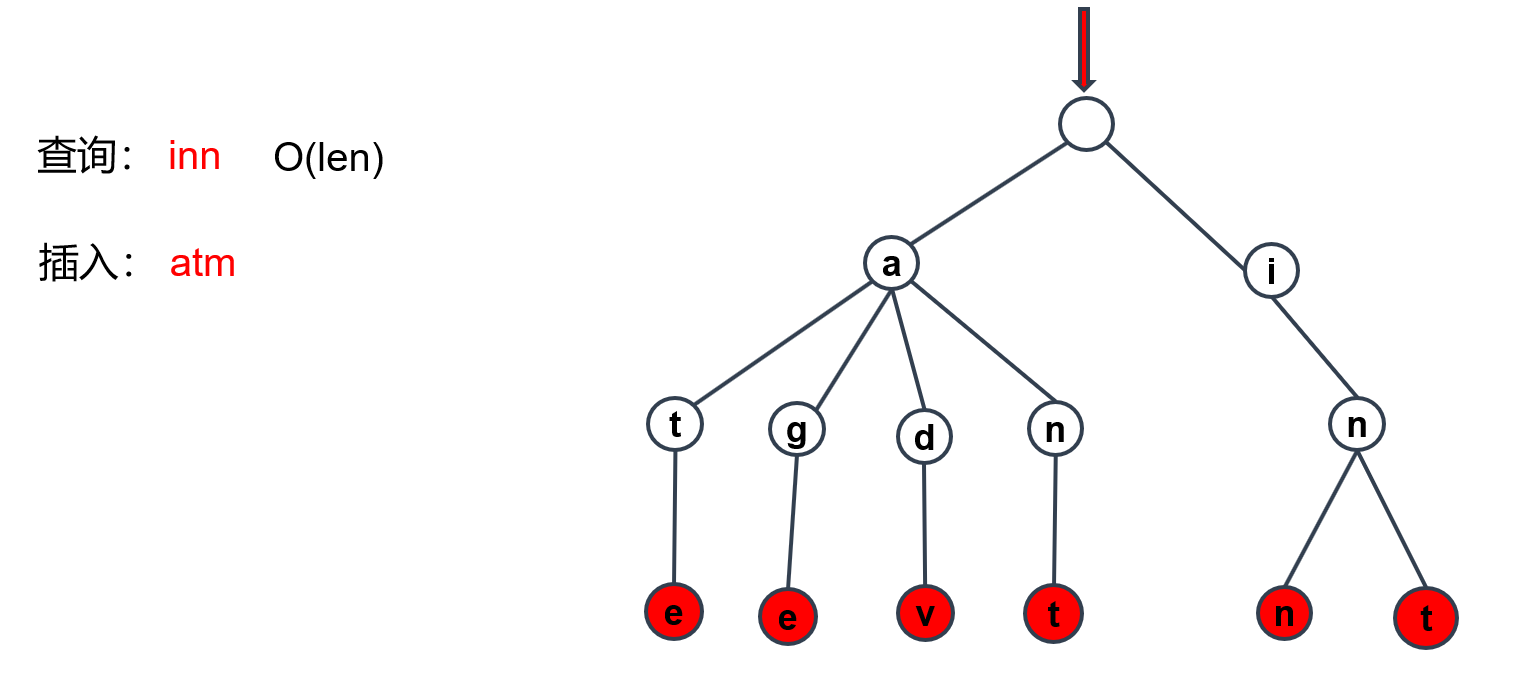
现在我们要插入新的字符串atm,那应该怎么做呢?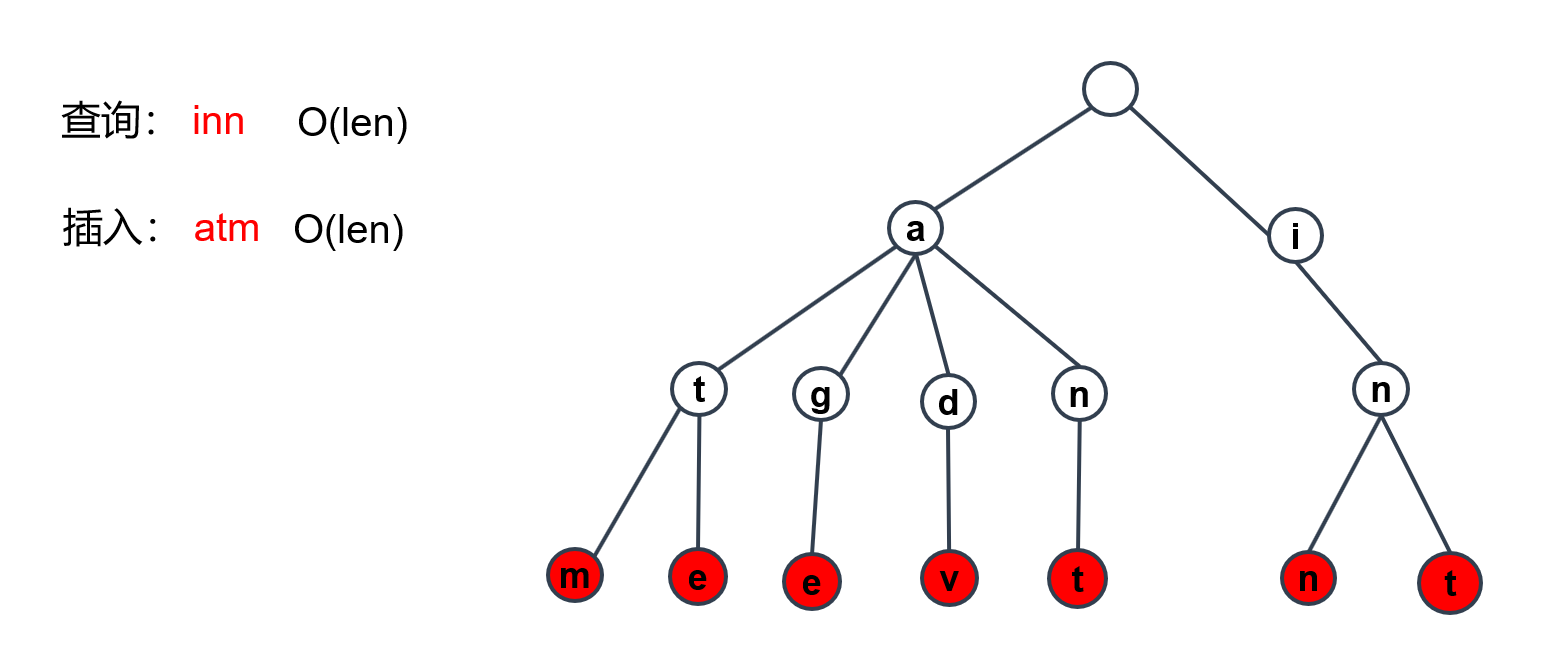
在走到t结点时,发现没有m结点,所以构造出m结点,并变为红色。
字典树的删除
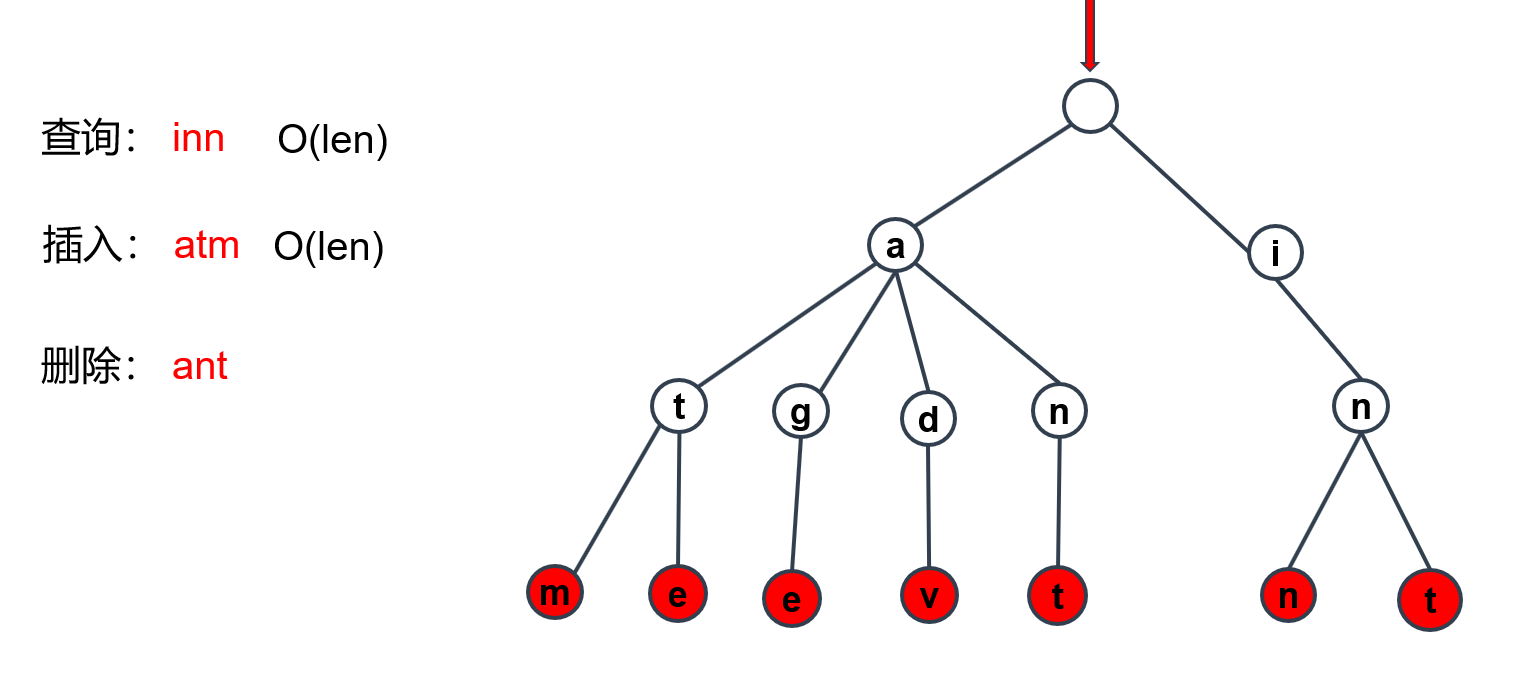
现在我们要删除字典树中的ant字符串,当然是从根节点开始去做一个查询。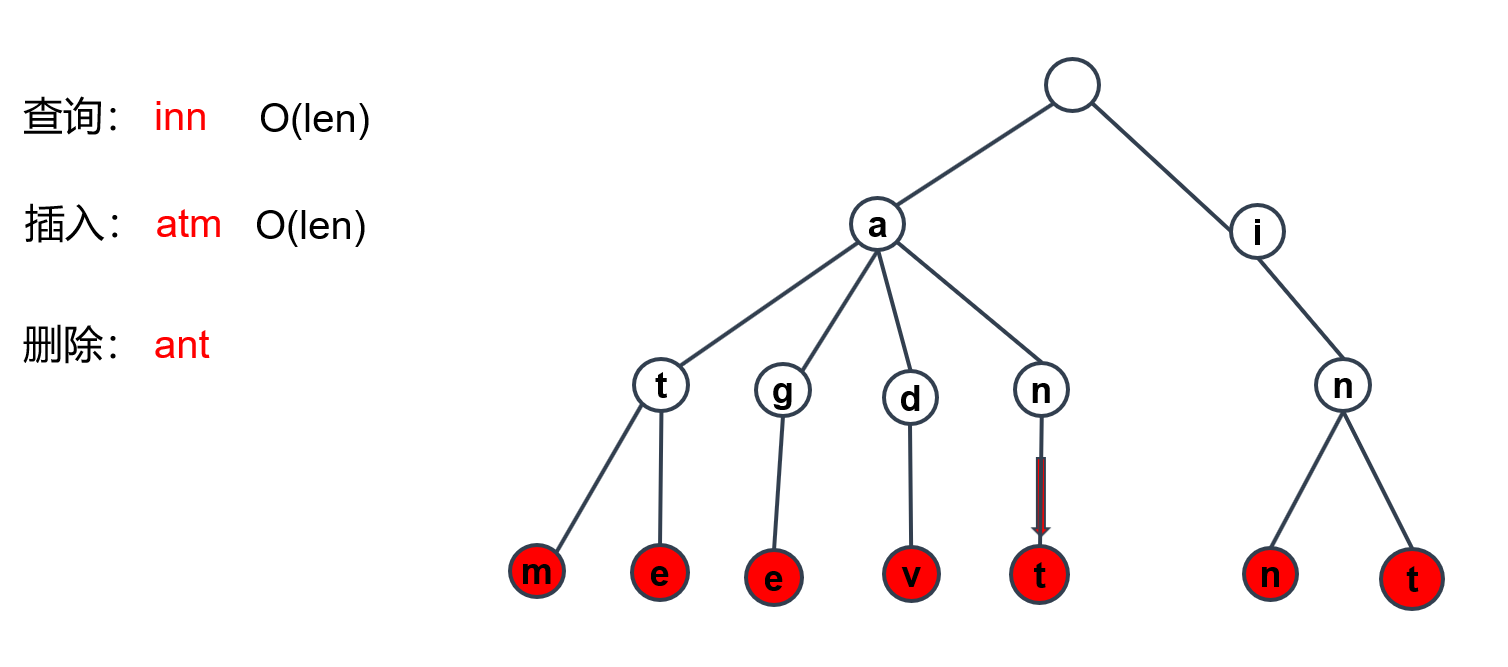
最后找到,结点t并且n结点也并没有其他分支,所以在删除时,会将n->t全部删除。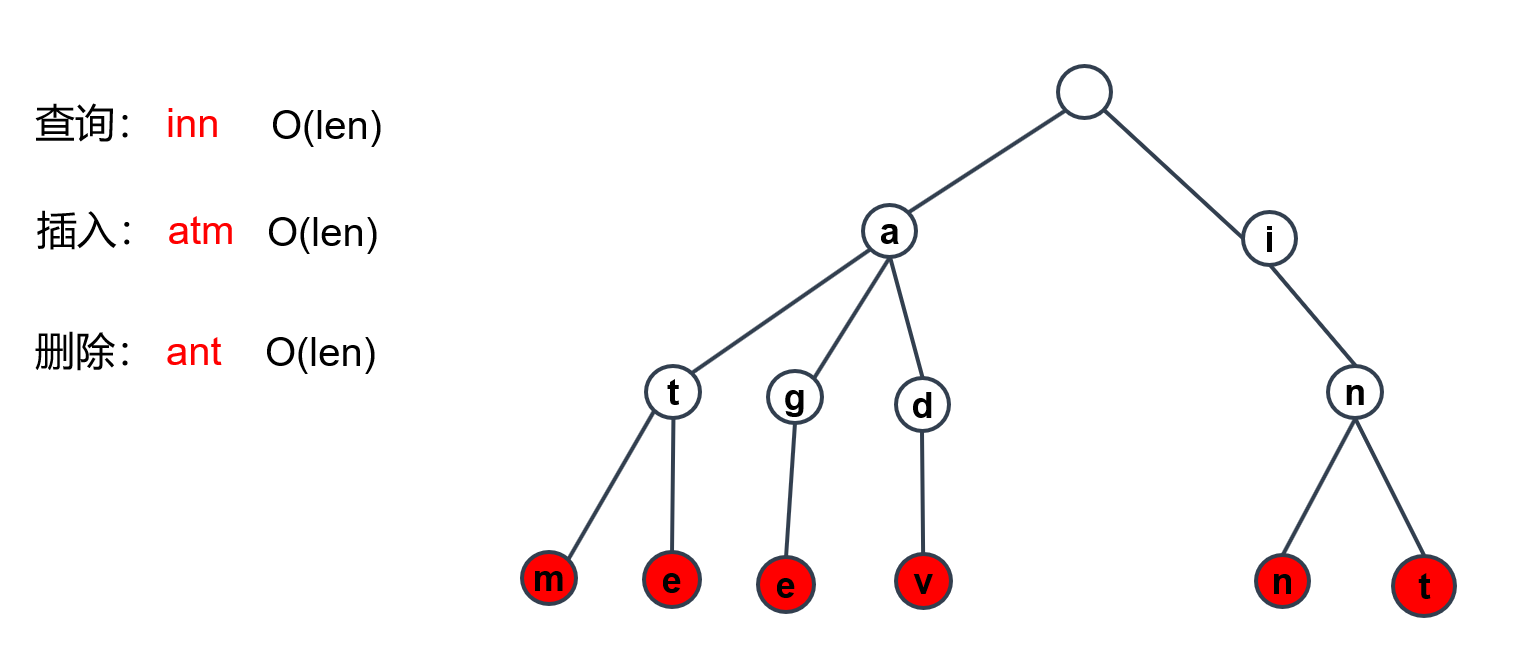
最后结果如图所示,时间复杂度也为O(len)。
字典树的应用
